Flower of Life Step by Step Drawing

The Math of The Flower of Life (+ implementing it in JavaScript)

Beginners: I promise if you can follow instructions you'll make it through this and be able to extend it on your own. I try to explain most concepts but if something doesn't make sense don't hesitate to just copy and paste :) The most important part of creative coding is making something work. I learned everything I know through copy/pasting and seeing what happens

Developers: This starts slow but ramps up at Drawing The Rest Of The Circles . You can just jump there and copy the code right above if you already know p5 and geometry basics

So what are we •actually• doing here? Believe it or not it's pretty much just what did above but with some math that fifteen year-olds know and I, as a grownup, totally had to google. The following is done in p5.js but the general principles apply everywhere.

Setting It Up

To build our Flower of Life we're going to use p5.js, an art library that makes 'coding accessible for artists, designers, educators, and beginners'.

Strictly for convenience we're going to do this in CodePen to prevent you from having to do setup work. Go ahead and click this link, adjust the screen so it looks like the screenshot below, and you can immediately start coding. Now, let's get to communing with everything!

Core Functions

The first thing we need to do is set up p5's essential functions, setup() and draw(). Pretty much anything you do in p5 requires these two so let's talk a little bit about what they do.

setup() is called first and defines some of the initial properties of our program. In our case this will be the size of the canvas and the frame rate, the number of times per second our image refreshes. Go ahead and type the following block in.

Quick note for beginners: Lines that begin with a `/` are not code but rather instructions or further explanation called comments. You can include them or not — they're there to educate :)

Next let's take a look at draw(). As the name implies this is where we put all of our instructions about what to draw. Right now let's just set a background color so we know everything is working.

Your First Circle

Okay cool. We've got ourselves a grey background but out of the void must come something… so let's draw our first circle.

P5 has a bunch of functions that help you draw shapes as long as you know some basic information about them. To draw an ellipse we just use a function called, wait for it, ellipse()!

Ellipse() takes three parameters, or pieces of information, inside its parentheses: the x coordinate of the shape's center, the y coordinate of the shape's center, and the diameter of the circle.

Let's add the following line to our draw() function

Looking good but maybe not the most exciting thing in the world. Let's get our second identical circle on the screen and turn everything into every thing!

The Second Circle

We know the second circle starts one radius away from the center of the first but we need to give our ellipse() function coordinates. So how do we find them?

There are several ways to do this but as we're working in Sacred Geometry might as well use the Pythagorean Theorem and really commit to the aesthetic and our cybermonk forebears.

The Pythagorean Theorem, a² + b² = c², is a way to find the length of the sides of any right triangle. This may not seem like it will help us find coordinates on a circle but imagine a triangle that starts at the center of our circle with a hypotenuse, the c in the theorem, with a length of 100, the radius we used in ellipse()

I said nice things about the protractor earlier but you can see it got less effective the more I used it

Let's arbitrarily decide we want to draw our second circle at a 60º angle from the center of the first. If we can find the length of the other two sides of this triangle all we have to do is tell p5 to draw a circle at them.

First let's find the length of the opposite side of the triangle which will represent our x coordinate. To get that we'll use the sin equation [you may remember it as the SOH part of SOHCAHTOA)

          sin(angle) = opposite/hypotenuse        

So in our case we can solve it like this

          // We know the angle, 60, and the length of the hypotenuse, 100, so we fill those in
sin(60) = Y / 100
// then we multiple both sides by 100 so we get the Y alone
100 * sin(60) = Y
// which leaves us with our answer ~ 86.6
86.6 = Y        

We do the same to find the value of X using the the cosine equation, the CAH part

          //We know the angle, 60, and the length of the hypotenuse, 100, so we fill those in
cos(60) = X / 100
// then we multiply both sides by 100 so we get the Xalone
100 * cos(60) = X
// which leaves us with our answer of ~ 50
50 = X        

Now that we know the length of both the X and Y sides of the triangle we can find the point of our first circle by adding these values to the center point of our first circle.

          // We're adding the values we found to 400 as that's where our first circle is centered
circle2.x = 400 + 50
circle2.y = 400 + 86.6        

We don't even need to do the math in our code as p5 has convenient sin() and cos() functions

and there we go! We've got ourselves two circles. If you want to play more with basic trig this site was super helpful and taught me a ton.

Your pen should look like this

The First Round Of Circles

We know the first part of the Flower of Life has six, equally spaced circles around the edge of another and we've just learned the formula for finding the coordinates of different parts of a circle's edge. As a circle has 360º all we need to do is place a circle every 60º (360/6) and we're good-to-go!

To do that we're going to use a for loop which just runs a bit of code as many times as we tell it to — check out out:

You'll notice we deleted the code for our second circle — that's because it was just a circle at 60º and we're drawing that here

Things don't look right, do they? That's because by default p5 assumes any angle value you're giving is in radians. We could convert the above formula to radians through a fairly simple formula but, honestly, it's easier to just tell p5 that we're working in degrees using the convenient angleMode() function. Go ahead and write

in your setup() function and pow! You've got yourself the right shape!

Or you do assuming it looks like this 😁

Adding some style

So now we've got some circles but, honestly, they don't look great. The Flower of Life is so visually compelling because you see where the circles overlap… and we've got here is a mess of white circles. As the guy at my deli says 'What up, Kahlo'

The HSB spectrum via p5's color article

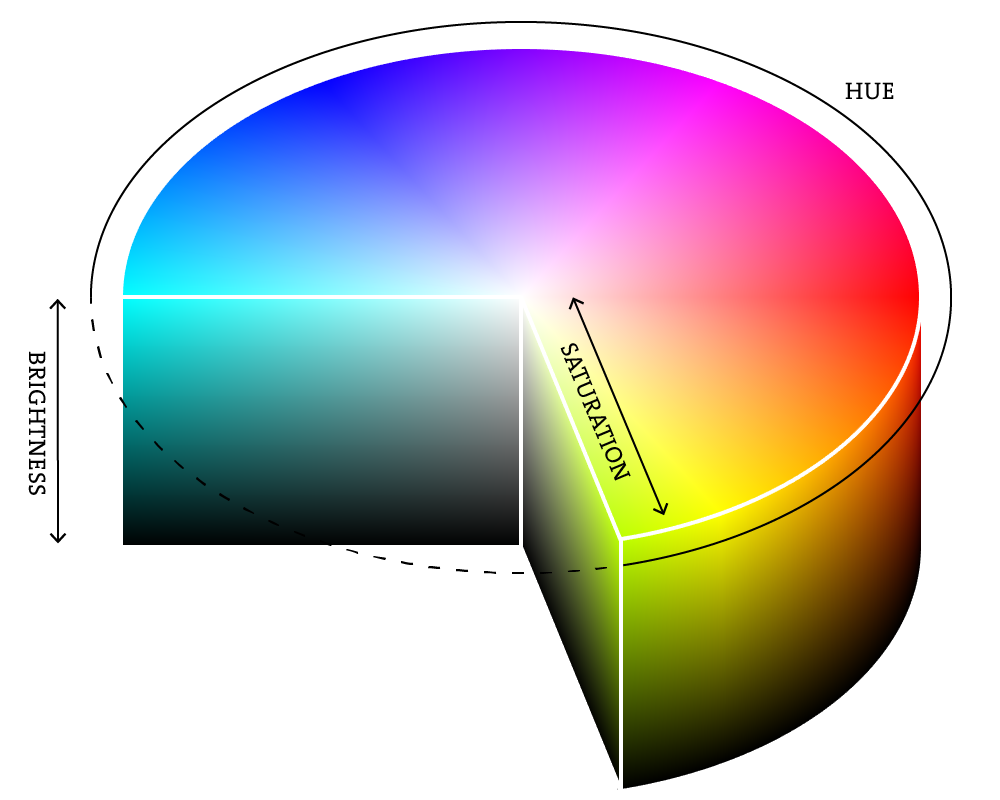
The first thing we want to do is to tell p5 we want to work in the Hue Saturation Brightness mode of color, or HSB. P5's site has a great article on color but all you really need to know that hue, what you might think of as the 'color' part of the color, is a visualized as a circle with values between 0 and 360 while brightness and saturation are given values between 0 and 100.

I know that's a little confusing so if the graph above doesn't help check out this great color picker by Hunor Marton Borbely I found. It should make it really clear.

HSB is a little unusual and you don't have to use it but I personally find it to be the best color system for animation and generative art. We'll see this in practice later. For now just go ahead and just add colorMode(HSB) to your setup() function.

Annnnnnd…. you'll notice no change at all :/

That's because to do that we need to tell p5 how we want to color our ellipses. We'll do that using the fill() draw() like this:

If HSB or for loops are new to you go ahead and play around with the fill value… maybe even try putting the `fill()` function in the for loop and seeing if you can get a different color each time!

Before we move onto drawing the next round of circles we should take a minute to clean things up and make sure my code is in sync with yours. I've done some light refactoring for readability.

Drawing The Rest Of The Circles

So now all that's left is repeating the above formula with with different radius values, right? That's what I thought and spent, uh, several days trying to figure out a formula that allowed me to easily do that. Feel free to try on your own but I'm almost certain no such formula exists :/

Our first set of circles can be easily drawn because they're all one radius away from the center of the initial circle. After our first round, however, the intersections are at totally different distances so a simple formula is out of the question.

So how do we do this? It requires going back to the initial description of this shape: for each circle we draw a new circle at its first clockwise point of intersection. And lucky for us some smart people have already figured out a way for us to find those points.

To do this we're going to be using Intersection of Two Circles by Paul Bourke (scroll down a bit on the linked page to see it.)

I spent so many hours with this graph that it's now my own personal sacred geometry

In conversational terms we're able to find the intersections point, p3, as long as we know the radii, r0 and r1, and centers, p0 and p1, of the intersecting circles. We do it like this:

• Use the Distance Formula to find the straight line distance between p0 and p1
• Use this equation to find the lengths of a and b
• Find the length of h using the the Pythagorean Theorem
• Use h to determine the x/y coordinates of the intersection

Let's try it with our circles:

We know that our first circle is at x = 400, y = 400; we derived that our second is at x = 500, y = 400; and both have a radius of 100.

Because we already know they intersect we can skip the first of Bourke's steps and immediately find the length of the chord that connects the two centers, d. To do that we'll use the distance formula:

          // Distance formula
d = √((x2-x1)^2 + (y2-y1)^2)
// For our example
d = √((500-400)^2 + (400 - 400)^2)
d = √(100^2 + 0^2)
d = √(10000)
d = 100        

So d, the line connecting our two circles, is 100px long.

Next we'll need to figure out how long just segment a is. We can do that using our new d value with the following equation:

          // General Formula
a = (r^2 - r^2 + d^2 ) / (2*d)          // For our example
a = (100^2 - 100^2 + 100^2) / 2 * 100
a = 100^2 / 2 * 100
a = 10000/200
a = 50        

Okay! Now we know the length of a and the length of r so finding h is just the Pythagorean Theorem

          //General Formula
h^2 = r^2 - d^2          // For our example
h^2 = 100^2 - 50^2
h = 100 - 50
h = 50                              

Now that we know this all we need to do is add our a length to our p0's x value and our h length to our p0's y value and we've got the coordinates p3 which are x = 450, y = 450.

These images got progressively harder to read, I know

Okay but that's a lot to do every time and, honestly, it's kind of confusing. Luckily the formula was converted into js so we can just use it without having to understand too much. Remember — creative coding is about getting it done :D

I've updated that function slightly so it's better suited for us but this is largely just an adaptation of 01AutoMonkey's work. Go ahead and take the following and just paste it into the bottom of your CodePen

Now when we want a circles intersection we can just call our new getIntersection() function, pass it the circles and radii we're curious about, and get the values without doing any work :)

Creating Classes

We've made some real progress but our current approach in draw() is going to get us into trouble. Right now we're calculating our ellipses in the for loop and not saving any information about them. See the problem? Our getIntersection() formula requires a reference to ur circles to tell us the intersection point. We can solve this by saving our circles in an array. While we're at let's stop calling our shapes circles and move to a more project-appropriate name and call them petals. Go ahead and update the top of your js file to include an allPetals array like this

For more information on arrays check out Daniel Shiffman's wonderful video

We need something to put in that array, though. So why not make a class for each new petal!

A class is really just a way to create multiple versions of a thing that share certain properties. If you really want to learn more Eloquent JavaScript has a great section on the topic… but for our purposes you can just know it's an easy way to make a bunch of similar things.

Let's make a class for our petals like this and toss it just below those global variables:

Now let's take advantage of all these cool new features and update our loop so instead of drawings petals with the ellipse() function we're storing information about them and saving them to the allPetals array.

But uhhh… now nothing is drawing? This seems like a lot of typing to have just gotten rid of everything?

That's because we're now saving our petals in the allPetals array but we're not actually doing anything with them :/

Let's fix that and see what classes can do all at once.

Doing Stuff With Classes

So we've got to tell something to use our ellipse() function so the shape is actually drawn… why not do it on that Petal class we just built!

Classes aren't just data like x, y, or index. They can also contain functions that do stuff with that data. Lets prove it by giving our Petal class the ability to draw itself by calling a function called drawPetal()

So now we can draw our petals but we're still not actually telling our program to draw them anywhere. Let's head to our draw() function and do just that:

But how are we going to draw those ellipses? We can do it easily by just iterating through our allPetals array and calling our new drawPetal() method on each thing inside of it. It looks like this

Simply this new code just tells our program to go through each petal in the order they're in our array and call the drawPetal() function on each of them. With that in our draw() function and we're... back to where we started... That's just coding sometimes 😓

We've just made a bunch of changes so before we move on why not do another quick checkin to make sure we're in sync:

You with me? Great. Now that we're through that detour let's make the most of all this new stuff.

Improving Performance

I'll admit I've been misleading you a bit — maybe you've ever noticed. I said this shape is just a pattern of

1. draw a circle
2. find the first thing that circle intersects
3. draw another circle there
4. repeat

But instead I've got us doing a for loop with a bunch of math. and we're doing a bunch of math that just isn't necessary. Let's refactor a bit and use that getIntersection() function.

First thing we should do is move our flower creation process out of the draw() function. That function runs 30 times per second which is great for things that change a lot, like animation, but terrible for things that never do, like math.

Let's make a function called getPetalPositions() and move all our our current creation stuff into it. It'll look like this:

This is really the same code we've been using — it's just in a different spot

now go ahead and call getPetalPositions() in setup() so this function only runs once when the program is first started.

That's better! You may have even noticed a slight speed increase in your browser. Coding is dangerous business 🤕

Using getIntersection()

Now let's finally use that getIntersection() function we worked so hard on. It'll look like there's a lot of new stuff here but really we're just restating the work we've already done

You'll notice we have an if statement that draws our 0th and 1st petals differently. This is because those are the two that set up all the rules every later petal follows. It makes the code a little bit less graceful than it otherwise might be but it's really just repurposing work we did earlier and this is just one of those annoying realities of adapting things from the real world into code :)

Drawing More Rounds

So I wish I could tell you we just increase the number in circleCount and call ourselves in harmony with all things but it's not that easy. They tell me enlightenment never is. 😓

You'll notice we've currently just hardcoded our getIntersection() to always give the intersection between the previous petal and the origin circle. This is true for the first six circle but, if you think back to our animations, petal 6 intersects with petal 1, not 0, and it's at that intersection that we need to draw the new circle.

So, uhhhh, how do we figure that out then? Well it ain't easy and I spent about a week drawing increasingly wacko graphs on a legal pad and writing serial killer-lite notes like 'something about 7 is wrong' and, for reasons I literally could not tell you, the word 'angle' in an octagon?

But eventually I found a general formula but, unfortunately, I had to derive it just by looking at the shape for awhile. (Though for what it's worth I think that struggle is literally the point of Sacred Geometry)

The general formula is: each new petal intersects with the petal one 'row' below itself unless it's rounding a corner (hitting a vertex) in which case it intersects with the vertex twice before continuing it's previous pattern.

Which like, what? Look, I said it's true; I didn't see it was clean. This is one of those things I think is easier if you see it for yourself.

Watch this a few times… and honestly if you want a better description of the way it moves lmk. Vertices in yellow

Let's take a look at what this will look like as pseudocode

          - Create a variable to store the index of the first intersected neighbor and set its value to 0            
- increase that value if the next neighbor is the final petal in a round
- increase that value if the next neighbor is not a vertex
                  

It's easy enough to handle steps one and two of our pseudocode but how do we know if something is a vertex? Do that we need one last bit of geometry.

Using atan2 to find angles

We can describe the Flower of Life as a circle with each petal located at some x/y coordinates some distance from the center. We already know the shapes center and the coordinates of our petals — we just don't know that petal's angle from center. Magically there's an existing function for that, it's called atan2() and you would not believe how happy I was to learn about it

Wikipedia's atan2() diagram

atan2, from 2 argument arctangent, is a formula that tells you the angle between the positive x axis (the right part of the horizontal line) and a specific point.

Getting a petal's angle should be as easy as passing the petals coordinates to that atan2(). So let's make a function, and call it getPetalAngle(), that does just that.

you'll notice a couple things that may be unusual in there so let's talk through them:

• In line 4we subtract our petal's x/y coordinates from those of the first ellipse. That's because our shape starts at (400, 400) and not (0, 0). This subtraction just shifts our final calculation to the right spot.
• In lines 6 & 8 we do some strange math on the result of atan2, also known as theta. This is because the result of atan2 is in radians and we've been working in degrees.
• In line 10 we round our end value. This isn't strictly necessary but pixels are note reality and we get some strange angles like 30.000000002 and rounding just makes things easier.

Now that we have a function that returns an angle for any x/y coordinates let's add it to our Petal constructor so that every new petal automatically gets its angle from center.

Drawing The Second Round

Now that we know the angle from center of each petal we can use it to increase our firstIntersection iterator and draw a second round of petals.

Let's head to our getPetalPosition() function and make the following changes:

The first big change is the offset calculation up top. The Flower of Life is made up of evenly-spaced circles of which there are six more even rotation through (i.e. the first round has six circles, the next twelve, the following eighteen, etc) so to find their spacing we just divide the number of degrees in a circle, 360º, by the number of circles we want to draw. We call that value an offset.

Once we have that offset value we use it in our vertexIntersection calculation which just tells us if our new petal is going to be intersecting a vertex.

As the Flower of Life is, effectively, a hexagon each of its vertices is 60º from the center. We can test if our new petal is going to be intersecting with a vertex by using the modulo operator which, honestly, just tells us what the remainder would be if you were to divide the two numbers. If our petal is hitting any angle other than one divisible by 60 we know it's not a vertex and can safely increase the iterator.

Drawing More Rounds

To be honest, though, our getPetalPositions() function is ugly and full of these weird things like that hard coded petalCount === 6 statement or the bizarre offset calculation. It would be easier if we could just tell our program how many rounds of petals we want to draw and not have to mess around with individual numbers. Luckily, we can! Let's hand back to the getPetalPositions() function and refactor it so it draws based on rounds rather than petalCount

You'll notice we're now focused on how many rounds we want to draw rather than how many petals. We no longer need to manually calculate offset or petals for each round values and instead we leave our program to work it out. Go ahead and pop any round count in here and you'll see you can make a huge number of petals with no additional work!

Tidying Up

You may notice our flower is getting bigger than our screen — lets decrease the size of the ellipseRadius so everything fits

See how easily everything changes? Variables are amazing.

Adding Some Life

Well, we've sort of done what we set out to do. You've researched the Flower of Life, understood the math behind it, and built your own. That's a big accomplishment and I bet there was a lot of new stuff in here so feel proud 🖤

But — for me at least — it seems like something is missing. It doesn't quite have as much style as I'd hope for so let's add some color.

The first thing we want to do is change up our Petal class so that each petal can have its own color rather than relying on the universal fill() function. To do that head to your petal class and add the following.

Two big changes to understand here:

• Our petal now takes round, fillColor, and strokeColor values
• When we call drawPetal() it now checks its instance for strokeColor and fillColor and uses those values, The reason we want to store these values in the instance rather than the draw() function is that it allows us to color and animate individually petals individually.

But where are those colors coming from? Variables of course :)

You'll notice we're using an array for fillColor — this allows us to apply consistent colors to different rounds

Now that we've got these colors let's actually pass them to our petals when we create them

That's a pretty straight forward update but you've probably noticed this strange code on line 22: fillColorArray[(roundCount + fillColorArray.length — 1) % fillColorArray.length]

We're once again using the modulo operator but this time we're telling our roundCount to, effectively, go back to zero if it's greater than the length of fillCountArray. It allows us to create as many rounds of petals as we want without having to worry about creating an entry in our color array for each.

Okay let's do another checkin to make sure we're both on the same page:

You've made it really far. Feel proud ❤

Animation

So far we've really just been using p5 as a drawing program but so much of its magic is in its ability to animate things. Let's try a simple example that should set you up to do all sorts of stuff on your own

But first a quick SEIZURE WARNING.

None of the steps I'm about to walk you through will cause rapid flashing. That said, we are working with a system that refreshes 30 times per second and you have arbitrary control over values. If you're not an experienced developer I'd suggest just copy pasting the final code and not manipulating things manually.

P5 makes it really easy to creating compelling animations, particularly when working in something as rules-based and psychedelic as Sacred Geometry. When you're still learning I find you can get the biggest impact by focusing on small changes that affect everything on screen the same way. Let's try changing two of our values to see this in practice.

Petal Hue

Earlier I suggested we use the HSB color system and here we finally get to see why. HSB allows you to uniformly change the appearance of colors using simple math which is ideal for us. Want to decrease the saturation of everything? Great! Just subtract from the s value across the board. Same with hue and brightness. If you want to see this in action check out the HSB Color Picker I linked earlier.

So let's try something simple like changing the hue of all of our petals every frame. This can be easily done in the draw() function:

We're again using the `modulo` operator because it "wraps" our numbers around so after reaching 360 our hue color goes back to 0and stays inside the HSB bounds.

Pretty cool, right? And all we're doing is taking the fill color we assigned earlier and adding 0.05 to the hue (the 0th value of the fillColor array) every frame.

Diameter

You could (and should!) do the same with the saturation and brightness values but I've found changing the diameter of the circle to be really fun and show the way the Flower of Life retains many of its properties even when it changes dramatically.

To change the diameter we can follow the exact same pattern as above and just add a little bit every frame. It'd look like this:

This is a neat effect but after awhile it lacks dynamism and aesthetically there's no real sense of pace. Personally, I think it would be better if it both expanded and contracted in a predictable way.

The most popular way of doing this in web animation is using the sin() function [amazing tutorial from Allison Parrish here] but in the interest of simplicity I'm going to show you an easier, if less graceful, way :)

Up in your global variables set up a new value called diameterIterator and set it to 0.2

then let's edit our draw() function so that our diameter grows until it's 150% its original size and shrinks until it's 50% of its original size

It's, like, really cool isn't it? Every frame we're just checking the size of the diameter and, if it's past our boundaries, flipping the iterator.

And with that you've set yourself to build some really cool stuff. Here's what your final code should look like:

Future Exploration

This is really just the start though. Here's some other things you could try:

• Animate only certain angles by limiting changes with

          if (petal.angle > x && petal.angle < y) {
            // do something cool like change the size or color
}        

• Change the position of certain indices

          if (petal.index === x) {
            petal.x += this
            petal.y += that
}        

• Convert our 2d ellipses to 3d cylinders
• Change the stroke color or remove it entirely
• Animate only parts the user hovers over

Pretty much anything you can identify you can arbitrarily change. I've even got the prototype that turns this into a generative music system using Tone.JS! Play around — I'd love to see what you come up with 😇

Flower of Life Step by Step Drawing

Source: https://medium.com/@brokyo/drawing-the-flower-of-life-22206fe36d02

Share this post